Postav si sám – „Záhadný“ dvojkužel
Učitel položí na laťkovou nakloněnou rovinu válec a on se kutálí dolů – nic překvapivého. Teď na stejnou dráhu položí dvojkužel – světe div se – JEDE NAHORU!

Školní pomůcka „záhadný kužel“ je typická pomůcka, která nadchne široké divácké okolí. Cena 500–600 Kč je však za dřevěný dvojkužel a tři šikovně spojené laťky poněkud vysoká. Pokud však své studenty nechcete o ukázku této pomůcky ochudit máte dvě možnosti: Sehnat sponzora, který nákup uhradí, nebo si pomůcku postavit z toho, co se ve škole najde. Tento článek by Vám měl pomoci pokud zvolíte variantu druhou. Pokud si chcete tuto pomůcku vyrobit, bylo by asi nejlepší začít tím, že si někde odměříte pomůcku již hotovou a vyrobíte přesnou kopii. To se mi však nepodařilo, tak jsem musel pomůcku navrhnout celou sám. Inspirací mi byla jen fotografie z nabídkového katalogu pomůcek a papírový model, který jsem si slepil pro ověřování svých fyzikálních závěrů.
Návrh pomůcky
Předpokládejme, že máme vyrobený dvojkužel známých rozměrů a laťku, ze které chceme vyrobit nakloněnou rovinu pro pohyb dvojkužele. Nejjednodušší možnost, jak sestavit tuto laťkovou dráhu vidíme na obrázku 2.
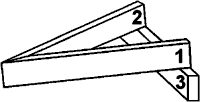
Naším úkolem je ze známých parametrů (s,d – rozměry kuželu a v – výška laťky – obr. 4) získat parametry hledané (L – délka použitých latěk 1 a 2, a Δ – šířka laťkové dráhy v nejvyšším místě – obr. 5). Podíváme-li se blíže na pohyb dvojkužele po nakloněné rovině a rozkreslíme si pohyb jeho těžiště, získáme obrázek 3.
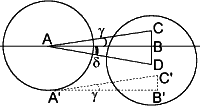
Trojúhelník A'B'C' představuje laťkovou dráhu, po které se dvojkužel pohybuje. Úsečka AC je dráhou těžiště, pokud by se dvojkužel „nepropadal“ laťkovou dráhou. Trojúhelníky ABC a A'B'C' jsou tedy shodné. Úsečka BD je snížení těžiště oproti vodorovnému směru – příčina pohybu dvojkužele po nakloněné dráze.
Pro následující výpočty a úvahy si délky jednotlivý úseček označme následujícím způsobem:
|AC| = ℓ, |AB| = ℓ' (průmět ℓ do podložky), |BC| = v (výška nakloněné dráhy – též výška použitých latěk), |BD| = y (propad těžiště oproti vodorovnému směru), |CD| = Y (propad těžiště oproti směru nakloněné dráhy).
Aby se pohyboval dvokužel směrem „nahoru“ po nakloněné rovině, musí jeho těžiště klesat. Tedy y > 0, nebo-li Y > v.
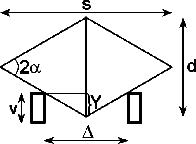
Vyjádříme-li si snížení polohy těžiště Y z parametrů dvojkužele (viz obr. 4) získáme podmínku:
kde d je průměr dvojkužele, s jeho šířka a Δ je šíře laťkové dráhy v nejvyšším místě dráhy.
Aby dvojkužel nenarazil svým obvodem o desku stolu dříve než dojede na kolec dráhu, musí být celkové snížení jeho těžiště Y menší než výška dvou latěk (jedna tvoří dráhu, druhou je na konci dráha podepřena – viz obr. 2). Z toho docházíme k podmínce pro maximální šířku laťkové dráhy Δ:
Hodnotu Δ tedy můžeme libovolně stanovit v daném rozmezí. Všimněte si, že v této podmínce se vůbec nevyskytuje délka dráhy ℓ, což by se zprvu mohlo zdát překvapivé. Uvědomme si však, že změnou délky dráhy ℓ se zmenšuje nejen úhel δ (snížení těžiště – obr. 3) ale i úhel γ (úhel nakloněné roviny). Kromě podmínky (2) je však třeba uvážit, že dvojkužel na konci by neměl laťkovou dráhou propadnout, tedy Δ < s.
Nyní se podíváme na podmínku pro délku dráhy ℓ a úhel snížení těžiště δ. Z hodnoty ℓ již pak získáme L délku laťky pro stavbu dráhy.
Z obrázku 3 plyne:
Dosazením a vyjádřením získáme podmínku pro ℓ, kde tg δ bude hrát roli parametru.
Úhel δ je naším parametrem, který charakterizuje, jak svižně se bude dvojkužel na laťkové dráze pohybovat.
Z délky ℓ lze podle obrázku 5 spočítat vnitřní délku laťky L; a tím i další potřebné parametry.
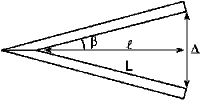
Z úvah o pravoúhlém trojúhelníku získáme pro vnitřní délku laťky ℓ vztah:
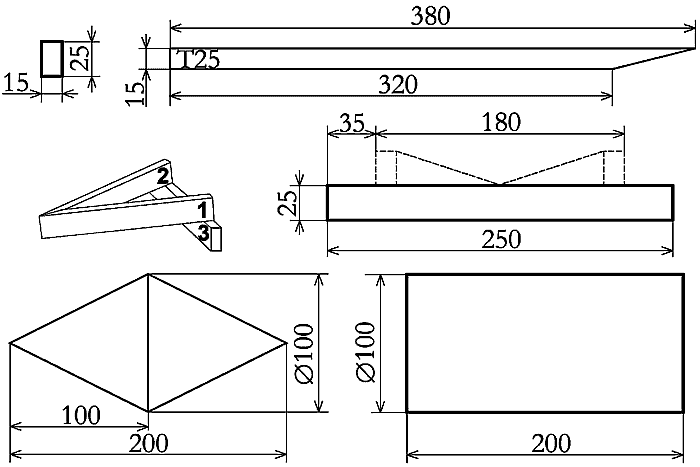
Ukažme si platnost těchto úvah a vzorců pro případ prezentovaný na výkresu (obr. 6). Pochopitelně díky obecné platnosti úvah a výpočtů lze rozměry modifikovat podle Vám dostupného materiálu, takže lze vyrobit pomůcku téměř libovolných rozměrů.
Máme-li dvojkužel o rozměrech d = 100 mm, s = 200 mm a laťku 15x25 mm, plyne z (2) podmínka: 100 < Δ < 200. S přihlédnutím na podmínku (3) a celkové řešení pomůcky volíme vnitřní vzdálenost latěk Δ = 150 mm.
Pro podmínku (3) potřebujeme zvolit úhel δ, který charakterizuje zrychlení dvojkužele po nakloněné rovině. Tvar této podmínky ukazuje, že je lepší zvolit přímo hodnotu tgδ. Zde jsem zvolil tgδ = 0,04 (tj. asi δ = 2,3°), tím získáme ℓ = 311,5 mm. Pro celkové rozměry ramen laťkové dráhy z toho plyne L = 320 mm a vnější délka laťky přibližně 380 mm. Tím jsme získali potřebné důležité rozměry a můžeme se pustit do stavby.
Stavba pomůcky
Většinu materiálu najdeme v dílně školního údržbáře, či jiného kutila ať již z řad učitelů nebo studentů. Problematickým místem je výroba dvojkužele. Potřebný špalík na výrobu jsem nakonec vyřešil slepením několika bukových odřezků z prkýnek, které jsem jako nepoužitelný odpad dostal od truhláře. K slepení posloužilo epoxidové lepidlo. Skutečným „zlatým hřebem“ však bylo soustružení dvojkužele. Nešlo tak ani o opracování výrobku, jako o jeho uchycení do soustruhu. Pokud budete dvojkužel soustružit ve vrtačkovém stojanu KOMBI, je asi nejlepší vyrobit dvojkužel bez špiček a ty pak rašplí a pilníkem dotvarovat v ruce. Máte-li štěstí, narazíte na šikovného soustružníka, který si s tím poradí pomocí jednoduchých přípravků a dokáže vysoustružit dvojkužel celý.
Zbývá pomůcku doplnit o válec, který po laťkové dráze jezdí dolů. Buď jej opět vysoustružíme, nebo použijeme jakoukoliv kulatinu, lepší je však průměr srovnatelný s kuželem.
Laťky nakloněné dráhy jsou lepeny tepelnou lepicí pistolí, jejíž hustá lepicí hmota může sloužit i jako tmel. K povrchové úpravě byl použit bezbarvý a lazurovací lak. Povrchy však lze nechat i bez nátěru. Ať se do výroby této pomůcky pustíte jakýmkoliv způsobem, odměnou Vaší snahy bude roztomilá fyzikální „hračka“, která nadchne každého.
Technický výkres
Autor článku: Miroslav Panoš
