Určení výšky Černé věže
Proč měřit to, co je již známo???
- Podívejte se na Černou věž – výrazným bodem je klenuté okno u zvonu. Každý, kdo se na tento bod podívá, dá za pravdu, že je asi ve třech čtvrtinách výšky věže. Při projektu „Vážení země“ jsme určili, že toto okno je ve výšce 39 m. Je-li toto okno ve třech čtvrtinách, jak všichni při prvním pohledu na věž tvrdí, byla by výška věže pouhých 52 m!!! (To je ale rozdíl téměř 30 metrů)
- Kdo řekl, že je Černá věž vysoká 80 m? Plechová cedule, na které je i chybný počet schodů na věž? Proč se nestát tou „autoritou“, která výšku potvrdí!
- Sbírky úloh (ať již matematiky či fyziky) jsou plné příkladů typu: Věž výšky h… pod úhlem α… apod. Tak proč si nevyřešit takový příklad pěkně naživo?
- Jak jinak by se stránky Fyzikální kabinet FyzKAB měly připojit k celoročním oslavám 750. let města Klatov, než strhnout pozornost na dominantu města, která dělá Klatovy Klatovami a na kterou se při oslavách, tak nějak trochu zapomnělo!

- Princip měření
- Měřicí aparatura
- Průběh měření - fotografie
- Výsledky měření
- Závěr
- Měření „konkurence“
Princip měření
1. metoda
První metoda vychází z klasického pravoúhlého trojúhelníku, kde jednu odvěsnu tvoří výška věže a druhou vzdálenost pozorovatele od věže. Změřením úhlu, pod kterým je z místa pozorovatele vidět špička věže a ze známé vzdálenosti od věže lze již poměrně jednoduše vyjádřit výšku věže. TOLIK ŘÍKÁ TEORIE!
Skutečnost je však trochu jiná:
- Černá věž nestojí na vodorovné podložce, jak bychom dle učebnicového příkladu potřebovali.
- Špička věže a pata věže není na stejné svislici – netvoří tedy jediný trojúhelník, jak bychom si přáli.
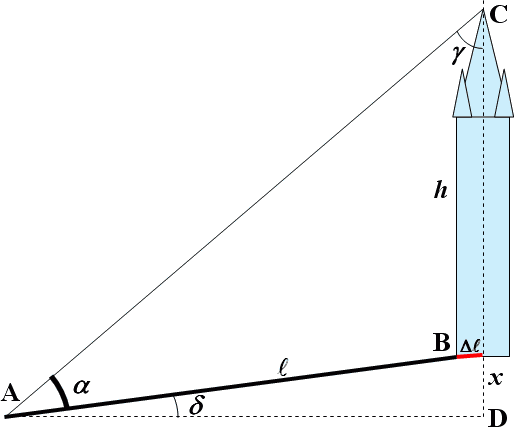
Celou situaci zachycuje obrázek číslo 1, kde jsou silně základní údaje, které budeme měřit. Označme si výšku věže h, vzdálenost pozorovatele od věže l a převýšení polohy paty věže nad místem pozorovatele x. Dále pak užité úhly jsou: α (resp. δ) úhel, pod kterým uvidíme špičku (resp. patu) věže. Pro přesné určení výšky však budeme ještě potřebovat šířku věže Δl (na obr. červeně) a pak již můžeme psát:
Víme-li, že součet úhlů v každém trojúhelníku činí 180°, tak z pravoúhlého trojúhelníku ADC plyne, že úhel γ (u vrcholu C) γ = 90°– (α + δ). Užitím sinové věty pro trojúhelník ABC, který má s trojúhelníkem ADC společný vrchol dostaneme výraz:
Úpravou výrazu (1.1) a užitím součtového vzorce pro výraz sin(90°– (α + δ)) dostaneme vztah (1.2):
Celá metoda se nám de facto „smrskla“ na co nejpřesnější určení úhlů α a δ.
2. metoda
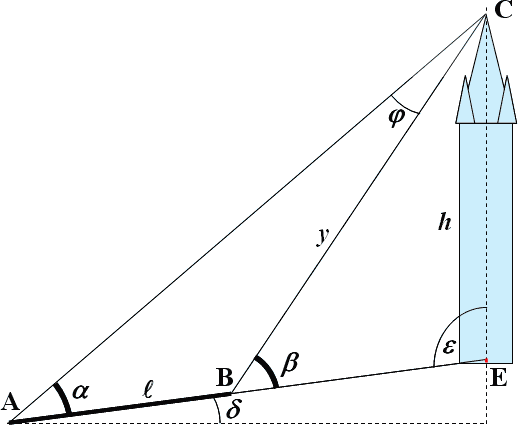
Druhá metoda je podobná. Abychom však eliminovali efekt tloušťky věže a také toho, že celá spojnice mezi místem pozorovatele a patou věže nemusí být přímka a proto určení její délky může být zatíženo chybou, použijeme postupu zobrazeného na obrázku 2. Metoda je složitější na odvození, ale doufejme, že nám poskytne lepší výsledek.
Použitím sinové věty v trojúhelníku ABC získáme:
Jednoduchou úvahou trigonometrickou úvahou určíme, že φ = β – α a vztah (2.1) lze přepsat do tvaru (2.2)
Ze vztahu (2.1) dokážeme určit vzdálenost y, kterou budeme potřebovat pro výpočet výšky věže – viz vztah (2.3) (opět užití sinové věty – nyní trojúhelník BEC).
Vyjádřením vzdálenosti y ze vztahu (2.2) a dosazením do (2.3) dostaneme výsledný vztah (2.4):
Chyba měření určení výšky věže při této metodě může vzniknout ve chvíli, kdy vzdálenost l bude určena na úseku, který bude jinak strmý (úhel δ) než je podložka věže – na obrázku č. 2 vyznačeno červeně. Díky tomu, že v Černé věži je průchod, ve kterém lze tento sklon zjisti a dopočítat a mělo by se podařit tuto chybu však korigovat.
Měřicí aparatura
Původním plánem pro měření bylo využití teodolitu zapůjčeného od některé z geodetických firem. Ukázalo se však, že oslovené firmy neměly moc pro náš experiment pochopení, ale především, že klasický teodolit neumí odečítat úhly ve svislém směru. Museli jsme tedy sestavit meřicí přístroj z toho, co se našlo doma.
Základnu našeho přístroje tvoří fotografický stativ. Na něm je nasazena nivelační hlavice určená k vodováze. Místo vodováhy je však v ní uchycen nastavitelný úhloměr zakoupený při akci „kutilské dny“ v jednou nejmenovaném supermarketu. Zaměřovací (optickou) část tvoří puškohled s nitkovým hledím připevněný na nastavitelném rameni úhloměru.





Postup měření pak bude jednoduchý. Pomocí nitkového kříže v dalekohledu zaměříme zadaný bod na Černé věži (patu resp. špičku) a na stupnici odečteme odpovídající úhel. Dosazením do vzorců (1.2) či (2.4) získáme základní odhad výšky. Několika násobným opakováním a započtením dalších korekcí určíme co nejpřesněji výšku Černé věže.
Průběh experimentu:
Průběh experimnetu lze charakterizovat povzdechem jednoho z účastníků:
Když je v listopadu 10 °C a fouká studenej vítr, vytáhnu ze skříně bundu a nadávám, že zima už je tady.
Když je stejná kosa v květnu, vyrazím měřit výšku Černé věže…
Fotografie z měření














Výsledky
První částí měření bylo zjištění přesnosti měřicího přístroje. Zjistili jsme skutečnou výšku daného místa na věži – spuštění pásma z okénka a porovnali jsme výsledek s výsledkem určeným naší metodou. Ve chvíli, kdy jsme zjistili, že se údaje v rámci stanovené odchylky shodují započali jsme samotné měření.
1. metoda
První metoda se po určení odhadu chyby ukázala jako přesnější – ano, ne vždy to složitější musí být přesnější – a tedy jsme se soustředili především na ní. V tabulce č. 1 jsou zaznamenány změřené údaje a určené výšky významných míst na věži.
| č. m. | ℓ/m | α/° | δ/° | h/m | Pozn. |
|---|---|---|---|---|---|
| 1 | 39,9 | 21 | 2 | 15,5 | 2. okno |
| 2 | 39,9 | 28 | 2 | 21,6 | 3. okno |
| 3 | 39,9 | 32 | 2 | 25,5 | 4. okno |
| 4 | 39,9 | 39 | 2 | 33,3 | 5. okno |
| 5 | 39,9 | 41 | 2 | 35,8 | 6. okno |
| 6 | 39,9 | 44 | 2 | 39,9 | okno zvonu (dolní okraj) |
| 7 | 39,9 | 49 | 2 | 48,2 | podlaha ochozu |
| 8 | 39,9 | 50 | 2 | 49,6 | horní okraj záhradlí ochozu |
| 9 | 39,9 | 61 | 2 | 76,9 | zlatá koule |
| 10 | 39,9 | 62 | 2 | 80,4 | špička |
| 11 | 61,9 | 51 | 4 | 83,9 | špička - jiné stanoviště |
tab. č. 1 - tabulka naměřených výšek významných bodů na černé věži
Přesnost metody byla určena jako necelá 3 %, což při výšce věže odpovídá chybě měření asi 2 m.
Výsledkem našeho měření první metodou je výška věže:
h = (82 ± 2) m
2. metoda
I přes nepříznivé povětrnostní podmínky (10 °C a silný vítr) jsme se rozhodli vyzkoušet i druhou metodu. Druhou metodu jsme však provedli jen zběžně, neboť již dopředu jsme věděli, že je méně přesná – při pohledu na vzorec (2.4) vidíme, že zde je ve jmenovateli rozdíl úhlů β a α. Díky tomu, že je tento rozdíl poměrně malý a určení každého z úhlů je cca 1°, je relativný chyba výsledku poměrně velká.
Následující tabulka obsahuje experimentální data naměřená při druhé metodě. I když bylo provedeno jen jediné měření, je vidět, že výsledek je docela uspokojivý.
| č.m. | ℓ/m | α/° | β/° | δ/° | h/m |
|---|---|---|---|---|---|
| 1 | 22 | 51 | 62 | 3 | 79,2 |
tab. č. 2 - tabulka výsledku druhé metody
Chyba měření je pochopitelně díky výše zmíněnému několikrát větší než u předešlé metody
Výsledkem našeho měření druhou metodou je výška věže:
h = (80 ± 10) m
Závěr
I přes ne zrovna vhodné povětrnostní podmínky jsme se pokusili změřit výšku Černé věže. Ověřili jsme si, že námi navrženou metodou (zejména metodou č. 1) lze i s aparaturou složenou z toho, co se dá doma najít, určit výšku docela přesně (rel. chyba do 3 %). Po zprůměrňování všech získaných hodnot jsme dospěli k výsledku, že Černá věž je od paty až ke špičce hromosvodu vysoká:
Oficiální hodnota výšky Černé věže je stanovena 81,6 m. Shoda naší hodnoty s touto výškou je více jak dobrá.
Zajímavým zjištěním je fakt, že zvon Vondra, který se nalézá ve výšce 40 metrů, je skutečně v polovině věže – což při prvém pohledu na věž není vůbec zřejmé. Zajímavé je i to, že výška ochozu je „pouhých“ 50 metrů, i když poměrně velká část Klatovan; je přesvědčena, že je ochoz až ve výšce cca 65 metrů.
V některých pramenech je uváděna výška Černé věže 76 m. Nyní víme, že to je výška konce střechy, resp. zlaté báně na věži.
Měření „konkurence“ (Jak se věže měří jinde)
Podívali jsme se po Internetu a hledali jsme jiné školní skupiny, které měřily výšku nějaké jiné věže. Jediný tým, který jsme našli byla skupina studentů z gymnázia v Náchodě.
