VÁŽENÍ ZEMĚ - Fyzikální kabinet FyzKAB

Cíl projektu: Určení hmotnosti Země

Místo konání: Černá věž - Klatovy,

Datum: 28.10.2008, 12.15 - 13.00 hod.

Motto:

Krása středoškolské fyziky je především v její hravosti, stejně tak jako je krása moderní pedagogiky ve zpracovávání atraktivních projektů. Projekt „Pojďte zvážit zeměkouli!“ spojuje obojí…

Popis metody měření:

Fyzikální základ zkoumaného efektu je postaven na učivu prvních dvou let základního kurzu středoškolské fyziky. Zpracování projektu, zejména jeho technické zabezpečení stejně tak jako odpovědnost při práci, pak pro studenty ročníků vyšších. Atraktivitu projektu dodává nejen jeho pojetí - zvážit zeměkouli - ale především i jeho provedení s využitím známé městské dominanty - Černé věže.

Určení hmotnosti zeměkoule vychází ze základního Newtonova vztahu (1) mezi gravitačním zrychlením a_g a hmotností M_Z gravitačního centra (Země).

(1)

Úpravou vztahu (1) lze tedy snadno pro hmotnost Země získat vztah (2):

(2)

Celá experimentální úloha se tedy redukuje „jen“ na přesné určení gravitačního zrychlení a_g.

Určení gravitačního zrychlení a_g:

Metoda obvyklá

Jednou z možností určení gravitačního zrychlení a_g, která se často používá a která je však nejen fyzikálně chybná a hlavně NEBEZPEČNÁ, je metoda volného pádu. V principu jde o pouštění malých hmotných kuliček z velké výšky.

Metoda použitá

Námi navrhovaná metoda je postavena na efektu zcela kultivovanějším, bezpečnějším a díky své „pomalosti“ i nesrovnatelně bezpečnějším. Měření je založeno na vytvoření obřího matematického kyvadla. Splnění podmínek pro model matematického kyvadla bohužel vyžaduje zcela specifické podmínky, kterých lze velmi dobře dosáhnout právě velkou délkou závěsu kyvadla.

Technická realizace pokusu

Obr. č. 1 - schéma technické realizace

Pro vytvoření obřího kyvadla jsme se rozhodli využít Černé věže (viz obr. 1). Díky rozměrům vzniklého kyvadla bude i při malé úhlové výchylce kyvadla (nutný požadavek pro matematické kyvadlo) výrazná výchylka délková závaží na noci závěsu.

Navrhované provedení celého pokusu (naznačeno na obrázku) je podřízeno bezpečnosti účastníků, spoluobčanů a institucí v okolí Černé věže, tak i pravidlu NULOVÉHO ZÁSAHU do konstrukce samotné stavby městské dominanty.

Celý pohyb kyvadla by měl být pozvolný a potřebný časový úsek je tak relativně dlouhý (cca 15 s) a díky tomu měřitelný s potřebnou přesností i bez speciální techniky. Měřeno bude vždy 10 kmitů a to několika stopkami a měřiteli. Celkový čas bude zprůměrován a pak vydělen deseti, tím by se mělo dosáhnout co nejpřesnějšího určení doby kmitu.

Mezi dobou kyvu T a tíhovým zrychlením a_G je pak platný vztah (3):

(3)

ze kterého lehkou úpravou získáme vztah pro tíhové zrychlení (4):

(4)

K získání potřebného gravitačního zrychlení a_g pro vztah (1) stačí určit zrychlení tíhové a_G, které se určí z co nejpřesněji změřené dobu kmitu matematického kyvadla (vzorec (4)) realizovaného v gravitačním poli Země.

Odvození vztahu mezi a_g a a_G

Pro spojení vztahů (2) a (4) potřebujeme najít vztah platný mezi zrychleními gravitačním a_g a tíhovým a_G. Na obrázku číslo 2 vidíme situaci mezi oběma zrychleními (Kvůli ilustraci vzájemného vztahu mezi veličinami nejsou velikosti vektorů ve skutečném vzájemném poměru.).

Obr. č. 2: Vztah mezi a_g a a_G

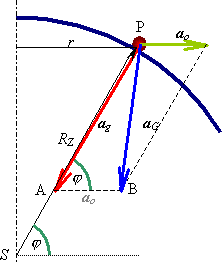
Mezi zrychleními a_g a a_G platí vztah (5) plynoucí z kosinové věty v trojúhelníku ABP, který vytvářejí společně se zrychlením odstředivým a_o:

(5)

což lze řešením této kvadratické rovnice (s ohledem na fyzikální význam kořenů) získáme pro zrychlení a_g finální vztah (6):

(6)

kde můžeme dosadit za zrychlení odstředivé jeho závislost na zeměpisné šířce místa pokusu P:

(7)

kde T_Z je doba jedné otáčky Země a r poloměr místní rovnoběžky.

Zemi budeme považovat za elipsoid s hlavní poloosou R_r (rovníkový poloměr) a vedlejší poloosou Rp (polární poloměr). Poloměr zvolené rovnoběžky pak lze vypočítat pomocí vzorce:

(8)

Stejně tak musíme určit „poloměr“ Země R_Z(pro vzorec (2)), který má na elipsoidu spíše význam vzdálenosti povrchu od středu.

(9)

Měření a výpočet

Pro samotné určení hmotnosti Země tedy využijeme vzorců (2), (4), (6), (7), (8) a (9). Čtenář toužící po obecném řešení si jako cvičení z úprav vzorců může tyto vzorce složit. Jelikož jsme celé měření zpracovávali v tabulkovém softwaru, kde výsledky jednotlivých parametrů a_g, a_G apod. chceme vidět a porovnávat, necháme vzorce samostatně.

Pro samotné měření jsme použili následující parametry:

R_r = 6378,135 km - rovníkový poloměr Země (zdroj: středoškolská učebnice zeměpisu),
R_p = 6356,750 km - polární poloměr Země (tamtéž),
T_Z = 23,934 h - přesná doba otáčky Země (tamtéž),
φ = 49,39463167 ° - severní šířka Černé věže (webové stránky MAPY.CZ, GPS přijímač),
κ = 6,6725985 .10^-11 N.kg^-2.m² - gravitační konstanta (MFCh tabulky)
l = 38,8 m - délka matematického kyvadla (změřeno dvěma způsoby)
T = viz následující tabulka - doba kmitu matematického kyvadla (experimentální určení)

č.m.	T	a_G	a_g	M_z
č.m.	s	m.s^–2	m.s^–2	kg
1	12,5060	9,794	9,808	5,969725 ·10²⁴
2	12,5080	9,791	9,805	5,967819 ·10²⁴
3	12,5075	9,792	9,806	5,968295 ·10²⁴
4	12,4933	9,814	9,828	5,981822 ·10²⁴
5	12,4900	9,819	9,833	5,985007 ·10²⁴
Průměr:				5,975 ·10²⁴ kg
Odchylka:				0,007 ·10²⁴ kg

M_Z = (5,975 ± 0,007) ·10²⁴ kg

Co na to pohled do historie?

V roce 1798 jako jeden z prvních vědců přesně spočítal hmotnost Země britský vědec Henry Cavendish (* 10. října 1731, † 24. února 1810). Použil k tomu torzní váhy, s jejichž pomocí změřil gravitační sílu působící mezi olověnými koulemi. Z ní odvodil gravitační konstantu a určil hmotnost Země. Jeho výpočty byly zpřesněny až ve 20. století, kdy se ukázalo, že Cavendishův výpočet odlišuje jen asi o 1 %.

Závěr:

V současnosti je nejlepší odhad hmotnosti Země asi 5,9736 .10²⁴ kg, což se od našeho výpočtu liší o 0,3 ‰!!!

Fotogalerie z měření:

Jak vidí Černou věž turisté I.	Jak vidí Černou věž turisté II.	Jak vidí Černou věž turisté III.
Členové experimentálního týmu	Dokumentaristický tým	Špičkové exp. vybavení
Spouštění měřicího lanka	Dopad lanka na zem	Lidé se začínali zastavovat…
…zastavovat…	…a zastavovat…	Montáž exp. aparatury I.
Montáž exp. aparatury II.	Montáž exp. aparatury III.	Zátiší s ramenem závěsu
Rameno závěsu	Měření délky závěsu	Balíme, jede se domů…