Užití integrálního počtu ve fyzice
Úlohy z CD-ROM ke studijnímu textu pro řešitele FO a ostatní zájemce o fyziku
© Mgr. Miroslava Jarešová, Prof. RNDr. Ivo Volf, CSc.
Studijní text „INTEGRÁLNÍ POČET VE FYZICE“ je velice pěkný text a lze jej použít pro výuku na fyzikálním semináři. Bohužel součástí tohoto textu byl i CD-ROM s příklady, na které je v textu odkazováno. Zatímco původní studijní text je ke stažení ve formě PDF souboru na mnoha fyzikálních stránkách, obsah CD-ROMu je akorát jen v dosti retro podobě na stránkách: Integrální počet ve fyzice.
Dovolili jsme si tedy čistě pro naše výukové účely převést část, kterou využíváme při výuce integrálů na fyzikálním semináři, do typograficky použitelnější podoby.
Cvičení 6:
Níže uvedené úlohy jsou uvedeny jako ukázkové s úplným řešením. Po projití těchto úloh bude ještě následovat Sada úloh k samostatnému řešení, u těchto úloh jsou už uvedeny pouze výsledky.
A) Obsah rovinného obrazce
Je-li funkce f spojitá a nezáporná na intervalu ⟨a; b⟩, je obsah S množiny na obrázku vpravo určen vztahem:
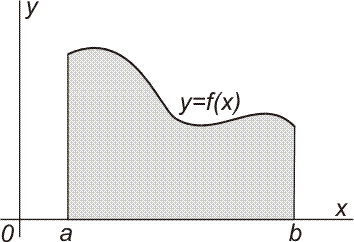
Jsou-li funkce f, g spojité na intervalu ⟨a; b⟩ je-li f(x) ≤ g(x) pro všechna x∈⟨a; b⟩, je obsah S množiny, vyšrafované na obrázku vpravo, určen vztahem:
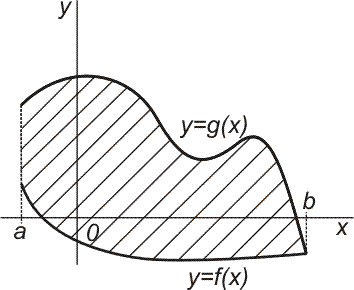
B) Objem rotačního tělesa
Je-li funkce y = f(x) spojitá a nezáporná na intervalu ⟨a; b⟩, je objem rotačního tělesa vzniklého rotací křivky f(x) kolem osy x (obrázek vpravo) určen vztahem:
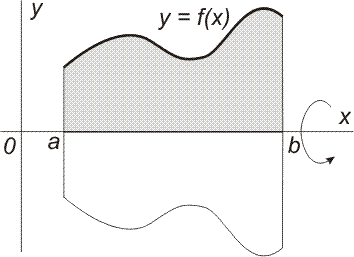
C) Obsah rotační plochy
Má-li funkce y = f(x) spojitou derivaci na intervalu ⟨a; b⟩ a je-li v tomto intervalu nezáporná, je obsah rotační plochy vzniklé rotací grafu funkce f(x) kolem osy x určen vztahem:
D) Délka křivky
Nechť je funkce y = f(x) spojitá na intervalu ⟨a; b⟩ a nechť má na intervalu ⟨a; b⟩ spojitou a neomezenou derivaci. Délka křivky, která je jejím grafem, je pak určena vztahem:
Užití určitého integrálu ve fyzice
a) Kinematika
- Je-li a(t), kde t∈⟨t0; t1⟩, zrychlení přímočarého pohybu v čase t, a je-li v0 rychlost pohybu v čase t0, je rychlost pohybu v(t) v čase t určena vztahem:
, t∈⟨t0; t1⟩
- Je-li v(t), kde t∈⟨t0; t1⟩, rychlost přímočarého pohybu v čase t a je-li s0 dráha pohybu v čase t0, je dráha s(t) v čase t určena vztahem:
, t∈⟨t0; t1⟩
Obdobné vztahy jako pro přímočarý pohyb platí i pro pohyb hmotného bodu po kružnici, tj.:
- Příklad 1
- Hmotný bod koná přímočarý pohyb tak, že jeho zrychlení s časem rovnoměrně roste a za prvních 10 s pohybu vzroste z nulové hodnoty na 5 m·s–2. Jaká je rychlost pohybu hmotného bodu v čase t = 10 s a jakou dráhu hmotný bod za tuto dobu urazil, jestliže v čase t = 0 s byl v klidu?
Pro závislost zrychlení na čase je možno psát:
, kde
Pro rychlost a dráhu pohybu potom dostáváme:
Za 10 s pohybu získal hmotný bod rychlost 25 m·s–1 a urazil dráhu 83,3 m.
b) Proměnná síla
Na element plochy působí tlaková síla .
Na celou plochu pak působí tlaková síla, která je dána součtem jednotlivých tlakových sil, tj.:
- Příklad 2
- Deska D, mající tvar parabolické úseče s výškou 20 m a délkou tětivy 4 m, je zavěšena v nádrži s vodou, jak ukazuje obrázek vpravo. Hladina vody splývá s osou x. Určete velikost síly, kterou působí voda na jednu stranu desky. Uvažujte g = 10 m·s–2, ρ = 1 000 kg·m–3.
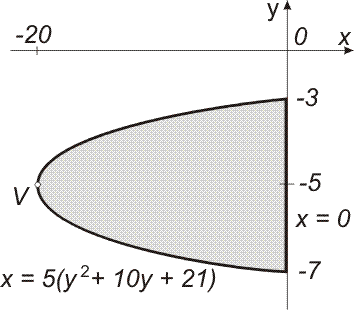
Určíme funkce f a g a meze y1 a y2. Vrchol parabolické úseče (viz obrázek) má souřadnice [–20; –5]. Protože osa paraboly je rovnoběžná s osou x, má tato parabola rovnici:
x + 20 = a (y + 5)2, kde a∈R
Protože na parabole leží body o souřadnicích [0; –3], musí platit:
0 + 20 = a (–3 + 5)2 ⇒ a = 5
Parabola má rovnici:
x + 20 = 5 (y + 5)2
Funkce f a g jsou:
g(y) = 0; y∈⟨–7; –3⟩
f(y) = 5 (y + 5)2 – 20 = 5 (y2 + 10y + 21); y∈⟨–7; –3⟩
Pro hledanou sílu pak dostáváme:
≐ 2,67 ·106 N
Kapalina působí na jednu stranu desky silou, jejíž velikost je přibližně 3 MN.
- Příklad 3 – síla působící na otáčející se tyč
- Homogenní válcová kovová tyč o hustotě ρ = 8 g·cm–3 a délce ℓ = 30 cm se otáčí kolem pevné osy procházející těžištěm tyče kolmo na směr délky úhlovou rychlostí ω. Jaká může být největší úhlová rychlost otáčení, jestliže největší dovolené napětí, kterému můžeme tyč v podélném směru vystavit, je σD = 60 MPa?
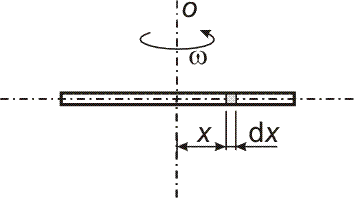
Celková síla, která působí v podélném směru na tyč se rovná součtu odstředivých sil, kterými vzdálenější části tyče působí na ty části tyče, které se nacházejí blíž k ose otáčení. Příspěvek elementu tyče, vyznačeného na obrázku vpravo, k celkové síle bude:
dF = xω2 dm = ρSω2 x dm, kde S je průřez tyče.
Celková síla potom bude:
.
Protože dovolené napětí: , můžeme psát:
Pro dané hodnoty ω = 832 rad·s–1.
Největší úhlová rychlost pro tyč může být 832 rad·s–1.
- Příklad 4 – síla působící v gravitačním poli
- Určete velikost gravitační síly, kterou na sebe navzájem působí hmotný bod o hmotnosti m1 a homogenní tyč délky ℓ a hmotnosti m2, jejíž hmotný střed má vzdálenost a od hmotného bodu a leží v prodloužení podélné osy tyče (viz obrázek).
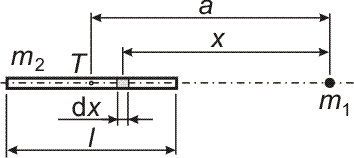
Nejprve určíme velikost síly dF, kterou na sebe vzájemně působí hmotný bod o hmotnosti m1 a element dm2 tyče. Jelikož element můžeme považovat za hmotný bod, můžeme použít základního vztahu – Newtonův gravitační zákon ve tvaru pro dva hmotné body:
Element tyče dm2 má tvar válečku o délce dx. Jelikož délková hustota tyče je je hmotnost elementu
Integrací přes všechny elementy tyče dostaneme:
,
c) Výpočet práce a energie
Práce síly F je dána integrálem ze skalárního součinu síly F a elementární dráhy ds. Je-li směr obou vektorů stejný, pak můžeme psát:
Bude-li síla F konstantní, pak , což je známý vztah.
- Příklad 5 – práce vykonaná při čerpání nádoby
- Vypočtěte práci, kterou musíme vykonat, abychom vyčerpali nádrž tvaru polokoule, je-li naplněna do poloviny vodou (viz obrázek). Poloměr je r = 2 m.
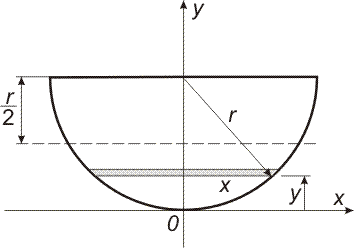
Zvolme si soustavu souřadnic podle obrázku. Element vody (vrstva vody o tloušťce dy – viz obrázek) o hmotnosti dm = πρx2dy musíme zvedat do výšky (r – y). Vykonáme tím práci:
Z rovnice kružnice dostaneme:
- Příklad 6 – práce vykonaná v elektrostatickém poli
- Vypočtěte práci, kterou musíme vykonat, abychom přenesli kladný jednotkový náboj Q1 = 1 C z nekonečna do bodu A, který je od bodového náboje Q = 1 000 C vzdálen o r = 1 m.
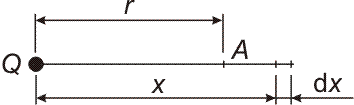
Ve vzdálenosti x si zvolme element vzdálenosti dx. Práce vykonaná na tomto elementu je dW = F dx.
Podle Coulombova zákona je:
Znaménko minus je zde proto, že musíme působit silou opačného směru než síla Coulombova. Odtud integrací:
protože
Pro dané hodnoty je W = 9·1012 J.
- Poznámka:
- Uvědomte si, co jsme vlastně vypočetli v obecném řešení předchozího příkladu. Připomeňme si definici potenciálu: číselně je roven práci, kterou musíme vykonat při přenesení kladného jednotkového náboje z nekonečna do daného místa v elektrickém poli (tj. do vzdálenosti r). Z toho vyplývá, že práce
určuje vlastně pro Q1 = 1 C potenciál bodového náboje Q, tj.:
- Příklad 7 – potenciál gravitačního pole
- Odvoďte vztah pro potenciál gravitačního pole ve vzdálenosti r od hmotného bodu o hmotnosti m.
Potenciál v gravitačním poli hmotného bodu o hmotnosti m určíme pomocí práce potřebné k přemístění hmotného bodu o hmotnosti m1 z nekonečna do bodu ve vzdálenosti r. Jelikož velikost gravitační síly Fg působící na hmotný bod o hmotnosti m1 je:
vypočteme práci potřebnou k přemístění bodu o hmotnosti m1 z nekonečna do vzdálenosti r integrálem (podobně jako v předchozím příkladu):
Hledaný potenciál
Gravitační potenciální energie
Newtonův gravitační zákon ve tvaru pro dva hmotné body platí také pro dvě homogenní koule nebo koule se středově souměrně rozloženou hustotou. Předpokládejme nyní, že jedno z těles je Země a druhé hmotný bod. I v tomto případě platí Newtonův gravitační zákon ve tvaru
Budeme uvažovat, že se hmotný bod přemístí z bodu A do bodu B (viz obrázek).
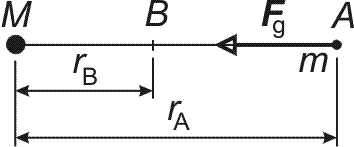
Určíme práci, kterou hmotný bod vykoná působením síly Fg.
Tuto práci určíme jako součet elementárních prací, tj. dW = Fg dr (Fg, dr mají stejný směr), potom:
Tato práce se rovná rozdílu gravitační potenciální energie hmotného bodu v počátečním a koncovém bodě trajektorie AB; nezávisí na tvaru trajektorie hmotného bodu mezi A a B.
Tyto poznatky využijeme při řešení následující úlohy.
- Příklad 8 – kinetická energie padajícího tělesa
- Vypočítejte kinetickou energii Ek tělesa o hmotnosti m, volně padajícího z výšky H, při jeho dopadu na zemský povrch, jestliže poloměr Země je R. Jaká by byla tato energie, kdyby H ≫ R? (Odpor vzduchu zanedbejte.)
Použijeme zákon zachování mechanické energie. Ve výšce H nad zemským povrchem, odkud těleso začíná volně padat, má těleso jen potenciální energii, jejíž hodnota je vzhledem k zemskému povrchu dána vztahem:
Při dopadu tělesa na zemský povrch má těleso jen kinetickou energii, pro kterou vzhledem k platnosti zákona zachování energie vyplývá
Tento vztah ještě můžeme upravit. Při povrchu Země:
Dosadíme-li do vztahu pro Ek, dostaneme:
Je-li H ≫ R, pak je zlomek:
- Příklad 9 – práce vykonaná při prodloužení pružiny
- Na pružině je zavěšeno závaží o hmotnosti m = 2 kg. Působíme-li na toto závaží silou F = 30 N svisle dolů, prodlouží se pružina o 66 cm. Určete práci síly F při prodloužení pružiny (uvažujte g = 10 ms–2).
Určíme tuhost pružiny k. Platí
Označme prodloužení způsobené tíhou závaží o hmotnosti m písmenem d. Platí:
Pro dané hodnoty: d = 0,44 m.
Pro práci při prodloužení pružiny platí vztah
Pro konkrétní údaje:
Práce síly při prodloužení pružiny o 66 cm je 23 J.
Přeměna elektrické energie v tepelnou
Prochází-li rezistorem o konstantním odporu R elektrický proud I(t); t∈⟨t0; t1⟩, určíme množství elektrické energie E, která se při tom přemění v tepelnou podle vztahu:
- Příklad 10
- Vypočítejte, kolik tepelné energie vznikne při průchodu proudu I = I0 sin ωt rezistorem o odporu R = 2 Ω po dobu t∈⟨t0; t1⟩, jestliže I0 = 20 A, ω = 314 rad·s–1, t∈⟨0 s; 7 s⟩.
- Návod: při výpočtu sestaveného integrálu použijte vztahu:
sin 2 ω t = 1 – cos 2 ω t 2 .
- Příklad 11
- Vypočítejte práci střídavého proudu I = I0 sin ωt ve vodiči s rezistorem R za jednu periodu T.
Postup bude obdobný jako v předchozím příkladu:
Dále použijeme substituci:
Potom:
- Poznámka:
- Z takto vypočtené práce lze jednoduše spočítat průměrný výkon (za jednu periodu).
Práce plynu
Při výpočtu práce ideálního plynu budeme používat následující vztahy:
1. termodynamický zákon ΔU = W + Q, který si upravíme pomocí diferenciálů na tvar dU = dQ + dW. Je-li dW (nebo dQ) záporná, soustava práci (nebo teplo) od svého okolí nepřijímá, ale odevzdává mu ji. Obvykle používáme značení dW' (dQ'), koná-li práci soustava (odevzdává-li teplo svému okolí). Platí vztahy dW = –dW', dQ = –dQ'.
Práce, kterou vykoná plyn při elementární změně svého objemu o dV, je dána vztahem dW' = p dV.
Po integraci vztahu pro práci dW' pak můžeme psát:
Dále budeme při výpočtech souvisejících s prací ideálního plynu používat stavovou rovnici ideálního plynu v různých tvarech, nejčastěji pak ve tvarech:
Výpočet práce ideálního plynu také velmi úzce souvisí s pojmy tepelná kapacita plynu. Zde rozlišujeme tepelnou kapacitu plynu za stálého objemu Cv a tepelnou kapacitu plynu za stálého tlaku Cp. Častěji pak pracujeme s tzv. molárními tepelnými kapacitami, které jsou definovány takto:
kde Mm je molární hmotnost plynu. Připomeňme si platnost vztahu Mm = Mr ·10–3.
Jestliže se při elementární stavové změně jednoho molu ideálního plynu jeho teplota změní o dT, jeho vnitřní energie U se změní
Uvažujeme-li plyn o hmotnosti m, pak obsahuje
Vztah mezi molární tepelnou kapacitou ideálního plynu za stálého tlaku a stálého objemu vyjadřují dvě rovnice:
- Mayerova rovnice
Cp – Cv = R,
pro měrné tepelné kapacity cp, cv pak platí:
- Rovnice, pomocí které je definována Poissonova konstanta κ
Z výše uvedených rovnic pak plyne pro Poissonovu konstantu κ vztah:
- Příklad 12
- Vzduch o tlaku 20 Pa je adiabaticky stlačen z 200 m3 na 50 m3. Určete výsledný tlak a velikost vykonané práce za předpokladu, že vzduch se chová jako ideální plyn.
Pro adiabatický děj platí pV κ = konst. (κ = 1,4 pro dvouatomový plyn). Označíme V1 = 200 m3, V2 = 50 m3, p1 = 20 Pa, pV κ = C.
Z rovnice pro adiabatický děj můžeme vyjádřit tlak p2 na konci děje:
Po dosazení p2 = 139,3 Pa.
Nyní vypočteme práci vykonanou při stlačování vzduchu. Platí:
Dále můžeme psát:
Pro dané hodnoty: W = 7411 J.
- Příklad 13
- Vypočtěte, kolik tepla se musí odejmout chlazením při izotermickém stlačení m = 45 g oxidu uhličitého CO2 teploty t1 = –15 °C a tlaku p1 = 0,23 MPa na tlak p2 = 0,58 MPa.
Při izotermickém ději se vnitřní energie ideálního plynu nemění. Při změně svého objemu z V1 na V2 vykoná plyn práci W', která se přemění na teplo. Z 1. termodynamického zákona dostaneme 0 = Q – W', z toho:
Za tlak dosadíme ze stavové rovnice výraz:
Potom:
Při izotermické změně platí podle Boylova-Mariottova zákona vztah:
Proto:
Protože p1 < p2, je tato práce (i přijaté teplo) záporné. Na izotermickou kompresi je třeba dodat kladnou práci W = –W', která se zcela přemění na teplo Q', které plyn vydá a které se chlazením plynu odebere. Pro toto teplo platí:
a tedy Q' = 2027 J.
Oxidu uhličitému se při chlazení musí odejmout 2027 J tepla.
- Příklad 14
- Vzduch o objemu V0 = 10 litrů, teplotě t0 = 0 °C a tlaku p0 = 0,1 MPa nejprve izotermicky stlačíme na objem V1 = 2 litry a potom adiabaticky rozepneme na objem V2 = 20 litrů. Jaká bude výsledná teplota vzduchu po ukončení této stavové změny a jaká celková práce se při tom spotřebuje? (κ = 1,4 pro vzduch)
Při izotermické změně bude mít vzduch tlak p1, objem V1 a teplotu T1. Pro tyto veličiny podle Boylova zákona platí:
Při adiabatické změně se změní tlak, objem i teplota plynu na hodnoty p2, V2, T2. Výslednou teplotu určíme užitím vztahu pro adiabatickou změnu a stavovou rovnici:
Po vydělení 1. rovnice 2. rovnicí dostaneme:
Protože T1 = T0, můžeme dále psát:
Pro dané hodnoty je T2 = 108,6 K, t2 = –164,4 °C.
Celková práce W', kterou plyn vykoná, se bude rovnat součtu prací získaných při izotermické změně W'1 a adiabatické změně W'2. Platí pro ně:
cv vyjádříme pomocí Mayerovy rovnice Cp = Cv + R, kam dosadíme:
Dostaneme:
Vztah pro W'2 pak můžeme dále upravit po dosazení za cv:
Podle stavové rovnice je však
Celková práce, kterou vykonal plyn, je pak rovna součtu těchto dvou prací, tj.:
Pro dané hodnoty: W' = –104 J.
Plyn tedy spotřeboval práci 104 J.
d) Těžiště tělesa
Ukážeme si, jak počítat polohu hmotného středu některých těles. Budeme předpokládat, že uvažované těleso je v homogenním tíhovém poli, tj. budeme mluvit o těžišti tělesa.
Připomeňme si základní podmínky pro výpočet těžiště tělesa:
- Těžiště tuhého tělesa je působiště tíhové síly působící na těleso v homogenním tíhovém poli.
- Moment výsledné tíhové síly vzhledem k libovolné ose musí být roven součtu momentů jednotlivých tíhových sil vzhledem k téže ose.
Na základě těchto podmínek můžeme např. psát:
odtud pak dostáváme pro souřadnice těžiště vztah:
Stejné vztahy platí i pro ostatní osy:
Uvažujeme-li těleso se spojitě rozloženou hmotností, pak můžeme psát:
kde jsme položili dm = ρ dV, ρ je hustota tělesa, dV objemový element, dm hmotnostní element. Vztahy bychom ještě mohli upravit užitím toho, že
- Příklad 15
- Stanovte polohu těžiště homogenního velmi tenkého drátu kruhového oblouku s poloměrem r a středovým úhlem 2α.
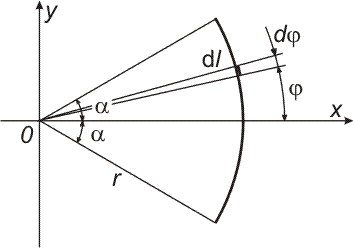
Ve zvolené soustavě souřadnic je yT = 0 m, zT = 0 m.
Z obrázku je vidět: ℓ = 2r α, x = r cos φ, dℓ = dφ.
Po dosazení do vztahu pro xT dostáváme:
- Příklad 16
- Určete polohu těžiště homogenního rotačního kužele výšky v a poloměru r.
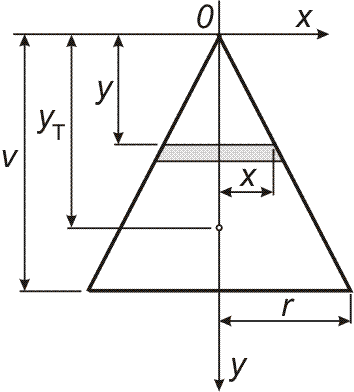
Dle obrázku můžeme psát:
Zvolme počátek soustavy souřadnic ve vrcholu kužele. Pak je xT = 0, zT = 0. Pro yT platí:
kde
Těžiště se nachází ve ¾ výšky od vrcholu kužele.
e) Výpočet momentu setrvačnosti
V této části si ukážeme, jak počítat moment setrvačnosti některých těles užitím integrálního počtu.
Doposud byl moment setrvačnosti J tuhého tělesa vzhledem k ose otáčení definován pomocí součtu
U těles se spojitě rozloženou látkou platí obdobný vztah:
kde jsme použili vztah dm = ρ dV.
Značka (m) resp. (V) u integrálu značí, že integrujeme přes celé těleso.
Výpočet momentu setrvačnosti těles vzhledem k libovolné ose otáčení ulehčují některé věty, především Steinerova věta:
kde J0 je moment setrvačnosti vzhledem k ose procházející těžištěm, a je vzdálenost osy otáčení od osy procházející těžištěm, m je hmotnost tělesa.
- Příklad 17
- Určete moment setrvačnosti homogenní tyče délky ℓ a hmotnosti m vzhledem k ose kolmé na směr délky tyče.
- procházející koncovým bodem tyče,
- procházející středem tyče.
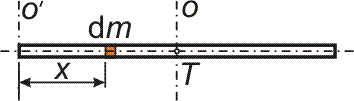
- Pro moment setrvačnosti vzhledem k ose o' můžeme psát
Potom
- 1. řešení – obdobně jako předchozí, pouze meze jinak (počítáme J0 vzhledem k o, ale x tentokrát měříme od osy o)
Po integraci dostaneme:
2. řešení – pomocí Steinerovy věty:
V případě b) oba postupy dávají stejný výsledek.
- Příklad 18
- Určete moment setrvačnosti homogenní kruhové desky hmotnosti m = 2 kg a poloměru r = 10 cm vzhledem k ose procházející středem desky kolmo na rovinu desky.
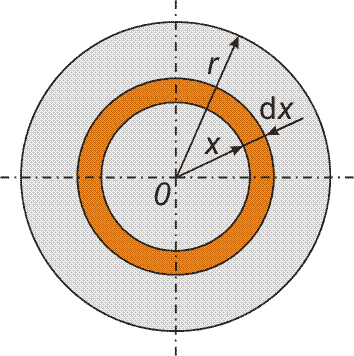
Zvolíme-li hmotný element desky ve tvaru mezikruží šířky dx, pak vzhledem k obrázku můžeme psát:
kde
- Příklad 19
- Určete moment setrvačnosti homogenní koule o poloměru r a hmotnosti m vzhledem k ose jdoucí středem koule.
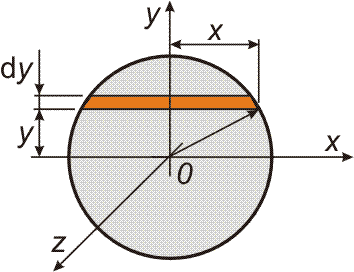
Zvolme si souřadnou osu y za osu rotace (obrázek). Kouli si rozdělíme řezy rovnoběžnými s rovinou (xz) na elementární kruhové destičky o poloměru x, tloušťce dy a hmotnosti m = πx2ρ dy.
Moment setrvačnosti tohoto elementu vzhledem k ose y je podle předchozího příkladu:
kde ρ je hustota materiálu koule.
Ve výše popsaném vztahu máme dvě proměnné. Platí však:
Po dosazení a integraci máme:
Jelikož hmotnost koule je
Úlohy na procvičování
(vhodné k samostatné práci)
- Příklad 1
- Jak velkou silou působí voda na boční obdélníkovou stěnu nádoby, jestliže vodorovná délka stěny a = 20 cm a svislá b = 15 cm a je-li nádoba zcela zaplněná vodou? (g = 9,81 m·s–2, ρ = 1000 kg·m–3)
[≐22,1 N]
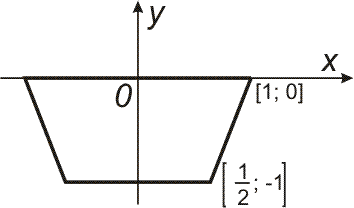
- Příklad 2
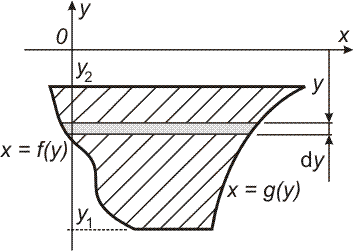
- Nádrž, jejímž průřezem je rovnoramenný lichoběžník, nakreslený na obrázku vpravo, je naplněna vodou. Jaká síla působí na jednu stěnu?
[
- Příklad 3
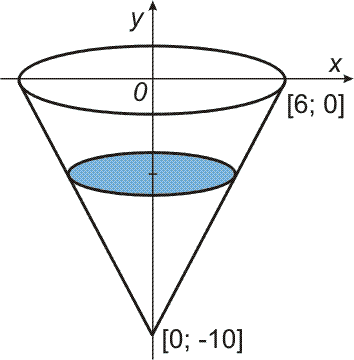
- Rotační kuželová nádoba o výšce 10 m a poloměru 6 m (nahoře) je plná vody (viz obrázek vpravo). Kolik práce se vykoná při vypumpování celého obsahu do výše okraje nádoby?
[3000 πρg = 92 372 520 J]
- Příklad 4
- Koule plave v kapalině hustoty ρ tak, že je do ní ponořená polovinou svého objemu. Jaká práce se vykoná při vytažení koule nad hladinu kapaliny, jestliže poloměr koule je R?
[
- Příklad 5
- O kolik se prodlouží tyč délky ℓ a průřezu S působením vlastní tíhy, je-li na jednom konci upevněná? Hustota materiálu je ρ, modul pružnosti v tahu je E. Uvažujte, že se jedná o pružnou deformaci – platí Hookův zákon.
[
- Příklad 6
- Řešte příklad 5 za předpokladu, že ke konci tyče je zavěšeno závaží o hmotnosti m.
[
- Příklad 7
- Síla, která je potřeba k prodloužení kovového sloupku délky a na délku a + x, se rovná
k x a
[
- Příklad 8
- Určete moment setrvačnosti homogenního rotačního válce o hmotnosti m a poloměru R vzhledem k podélné ose válce.
[
- Příklad 9
- Dokažte pomocí integrálního počtu, že těžiště rovnostranného trojúhelníka je ve vzdálenosti ⅓ výšky od základny.
- Příklad 10
- Střední hodnota
I S = 2 T ∫ 0 T 2 i d t ω = 2 π T
[
- Příklad 11
- Tlak a objem plynu jsou vázány vztahem pV κ = C, kde κ = 1,4; C je konstanta.
- Vypočtěte práci vykonanou stlačením 1024 m3 plynu tlakem 18 Pa na objem 243 m3.
- Ukažte, že práce vykonaná stlačením plynu s tlakem p1 z objemu V1 na objem V2 je
5 2 p 1 V 1 [ ( V 1 V 2 ) 2 5 – 1 ]
[a)
- Příklad 12
- Kolik tepla je třeba na izotermickou expanzi 2 litrů vodíku o tlaku 0,08 MPa na čtyřnásobný objem? Jaký bude výsledný tlak?
[
