Zpracování experimentálních dat – PŘÍMÉ MĚŘENÍ

Při použití přímé metody měření je výstupem přímo údaj hodnoty měřené veličiny v příslušných jednotkách. Je to tedy taková metoda měření, kdy je hodnota měřené veličiny získávána přímo, aniž je zapotřebí dodatečně provádět výpočty spočívající na závislosti měřené veličiny na veličinách jiného druhu.

Jinými slovy:: U přímé metody měření (přímého měření) zjišťujeme hodnotu fyzikální veličiny přímo odečtením na stupnici použitého měřidla, např. měření teploty teploměrem, měření délky pravítkem, měření elektrického napětí voltmetrem…

Výstupen našeho měření zpravidla bývá tabulka několika hodnot přímo reprezentujících měřenou veličinu. Tyto údaje obvykle musíme statisticky zpracovat a získat jako výsledek hodnotu určité „střední“ hodnoty (zpravidla aritmetický průměr) a hodnotu „nejistoty“ výsledku (tzv. chyba, či odchylka).

Ukážeme si to na konkrétním příkladu.

Ilustrační příklad:

Při měření délky drátu, na němž bylo zavěšeno závaží, byla získána následující data (viz tabulka) Zpracujte tyto data měření.

č. m.	ℓ / mm
1	518,9
2	520,0
3	519,8
4	520,4
5	519,6
6	520,1
7	520,0
8	520,2
9	519,7
10	519,8

Tab. č. 1 – délka drátu

Řešení:

Určení aritmetického průměru

V první řadě určíme aritmetický průměr naměřených hodnot. Aritmetický průměr označujeme pruhem nad označením veličiny a je dán vzorcem:

ℓ = \frac{ℓ_{1} + ℓ_{1} + \dots + ℓ_{N}}{N} = \frac{1}{N} \sum_{i = 1}^{N} ℓ_{i},

(1)

kde ℓ₁, ℓ₂… jsou jednotlivé hodnoty měření a N je celkový počet měření.

V našem příkladu dosazením hodnot z tabulky č. 1 do vzorce (1) dospějeme k hodnotě:

ℓ = 519,85 mm.

Určení odchylky měření

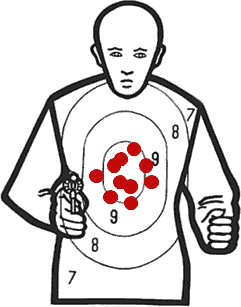
Je otázkou, s jakou přesností jsme tuto hodnotu určili? Tento problém nám ilustrují dva následující obrázky. V obou případech je střední hodnota (aritmetický průměr) zásahů někde ve středu terče, ale je jasné, že rozptyl zásahů je zcela rozdílný.

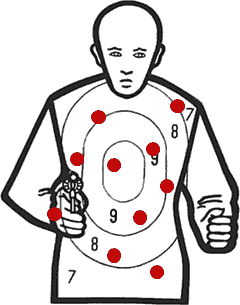Obr. č. 1 – ukázka různého rozptylu při stejné střední hodnotě

Stejně jako u rozptylu střelby, lze podobnou veličinu zavést i v případě přesnosti měření. Později poznáme a naučíme se korektní statistické veličiny. Nyní nám poslouží trochu zjednodušená, leč zcela dostačující veličina, které budeme říkat průměrná odchylka.

Z matematiky víme, že absolutní hodnota rozdílu dvou čísel nám určuje jejich vzdálenost. Vyneseme si tedy do tabulky tyto „vzdálenosti“ dané naměřené hodnoty od aritmetického průměru. Do třetího sloupce tedy spočítáme jednotlivé výrazy dílčích odchylek Δℓ_i, kde:

Δℓ_i = |ℓ_i – ℓ|

Dostaneme následující tabulku:

č. m.	ℓ / mm	Δℓ_i / mm
1	518,9	0,95
2	520,0	0,15
3	519,8	0,05
4	520,4	0,55
5	519,6	0,25
6	520,1	0,25
7	520,0	0,15
8	520,2	0,35
9	519,7	0,15
10	519,8	0,05

ℓ = 519,85 mm
Tab. č. 2 – tabulka exp. hodnot s aritmetickým průměrem a dílčími absolutními odchylkami

V tabulce č. 2 vidíme, jak se jednotlivé naměřené hodnoty odlišují od průměru. Jako určitou míru přesnosti našeho měření budeme právě považovat zmíněnou průměrnou odchylku, které je definována následujícím vztahem:

Δℓ = \frac{| ℓ_{1} - \overset{—}{ℓ} | + | ℓ_{2} - \overset{—}{ℓ} | + \dots + | ℓ_{N} - \overset{—}{ℓ} |}{N}

Δℓ = \frac{1}{N} \sum_{i = 1}^{N} | ℓ_{i} - \overset{—}{ℓ} |

(2)

Ze vzorce (2) vidíme, že průměrná odchylka je aritmetickým průměrem všech odchylek jednotlivých měření. Také si všimněte, že i když je tato odchylka dána jako aritmetický průměr, nebudeme ji označovat pruhem nad její značkou.

Vzorec (2) tedy použijeme pro určení průměrné chyby našich měření a získáme výslednou průměrnou chybu našeho přímého měření:

Δℓ = 0,29 mm.

Vyřazení hrubých chyb

Podíváme-li se na jednotlivé odchylky měření ve třetím sloupci tabulky, vidíme, že hned první hodnota má oproti ostatním poměrně velkou odchylku (chybu). Tuto skutečnost můžeme ilustrovat i grafickým zobrazením v následujícím grafu:

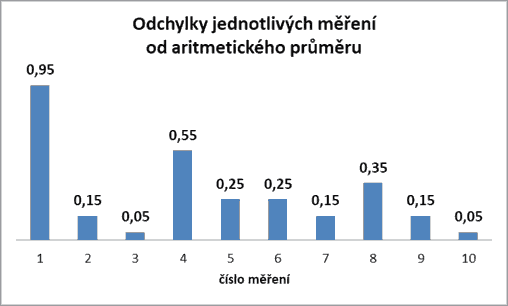
Graf č. 1 – grafické znázornění odchylek jednotlivých měření od aritmetického průměru

Na grafu č. 1 vidíme, že odchylka první naměřené hodnoty je téměř dvojnásobná, než je další menší odchylka (odchylka měření č. 4). Obdobně je vidět, že odchylka měření č. 4 je také poměrně velká zbylým odchylkám. V případě měření č. 1 máme tedy asi podezření na hrubou chybu. Otázkou je, zda je i měření č. 4 hrubou chybou, či již nikoliv. Potřebujeme tedy určité kritérium, které nám řekne, kterou hodnotu budeme považovat za hrubou chybu a můžeme ji tedy ze souboru vyndat a naopak kterou lze považovat za hodnotu validní.

Stanovení tohoto kritéria je poměrně matematicky obtížné a přesahuje matematické znalosti studentů prvního ročníku. Budeme si pamatovat, že takový způsob existuje a jednou, budeme-li mít to štěstí, se jej naučíme. Nyní pro naše běžné potřeby budeme využívat následujícího velmi zjednodušeného postupu:

Stanovíme si určitou hranici, kterou pokud odchylka měření překročí, budeme dané měření považovat za hrubou chybu. Tuto hranici (tzv. krajní chybu nebo též mezní chybu) si stanovíme jako trojnásobek průměrné odchylky:
(POZN: Později budeme používat tzv. směrodatnou odchylku a případný násobek této odchylky bude dán tzv. Studentovým součinitelem.)

3 · Δℓ = 0,87 mm

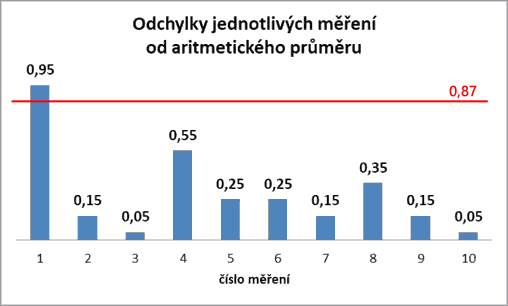
Graf č. 2 – grafické vyznačení krajní (mezní) odchylky v porovnání s jednotlivými odchylkami měření

Vidíme, naměřená hodnota číslo 1 má opravdu odchylku větší! Lze ji tedy považovat za htubou chybu.

Na základě právě zvoleného kritéria ji tedy můžeme ze souboru vyřadit. Dostaneme následující tabulku (Tab. č. 3) experimentálních hodnot:

č. m.	ℓ / mm	Δℓ_i / mm
1	520,0	0,04
2	519,8	0,16
3	520,4	0,44
4	519,6	0,36
5	520,1	0,14
6	520,0	0,04
7	520,2	0,24
8	519,7	0,26
9	519,8	0,16

ℓ = 519,95 mm
Tab. č. 3 – tabulka exp. hodnot po vynechání hrubé chyby a novém přepočítání aritmetického průměru a odchylek

Přesně podle předchozího postupu, tj. určením aritmetického průměru vzorcem (1), vytvořením třetího sloupce odchylek a určením průměrné odchylky dle (2), získáme nový aritmetický průměr a průměrnou odchylku.

ℓ = 519,95 mm, Δℓ ≐ 0,205 mm

Opět stanovíme krajní chybu jako trojnásobek průměrné odchylky: 3 · Δℓ ≐ 0,615 mm.

Vidíme, že již žádnou z naměřených hodnot nelze dle našeho kritéria prohlásit za hrubou chybu. Lze tedy považovat zpracování získaných experimentálních hodnot za hotové.

Zápis výsledku

Získaný výsledek již nyní jen zaokrouhlíme a zapíšeme ve správném tvaru. Hodnoty v mezivýpočtech (pokud možno!) nezaokrouhlujeme!

Obecně platí:

Výsledná odchylka u hlavního výsledku (tj. ten, se kterým se již nebude dále pracovat), se zaokrouhlí na první platnou cifru.
Výsledek se pak zaokrouhlí na stejný počet desetinných míst, jako je odchylka měření.

Příklady zaokrouhlení na 1. platnou cifru:

číslo	Zaokrouhleno na 1. platnou cifru
16,125	20
1 120	1 000
0,016 23	0,02
0,21	0,2
0,000 0543 21	0,000 05

Tab. č. 4 – ukázka zaokrouhlení čísla na 1. cifru

V našem příkladu tedy odchylku zaokrouhlíme na hodnotu 0,2 mm a výsledek tedy zaokrouhlíme na první desetinné místo. Hlavní výsledek našeho měření pak bude mít následující tvar:

ℓ = (520,0 ± 0,2) mm

Obecný postup při zpracování přímého měření veličiny X:

Spočítáme aritmetický průměr X .
Určíme průměrnou odchylku ΔX.
Vyloučíme ze souboru hrubé chyby a zopakujeme kroky 1–2.
Zaokrouhlíme odchylku a následně aritmetický průměr.
Zapíšeme výsledek ve tvaru X = (X ± ΔX) jednotek

Odstrašující případy špatného zápisu výsledků:

Nesprávný zápis	Co je špatně	Správný zápis
k = (92,432 31 ± 2,450 661) N/m	není zaokrouhleno	k = (92 ± 2) N/m
R = (1 653,2 ± 19,3) Ω	není zaokrouhleno	R = (1 650 ± 20) Ω
m = (198,435 1 ± 0,04) g	m není zaokrouhleno	m = (198,44 ± 0,04) g
b = (0,004 60 ± 0,000 042 4) m	není zaokrouhleno, příliš mnoho nul	b = (4,60 ± 0,04) ·10^–3 m b = (4,60 ± 0,04) mm
R = (1 600 000 ± 300 000) Ω	příliš mnoho nul	R = (1,6 ± 0,3) MΩ
E = (1,639 ·10³ ± 3) MPa	různé řády	E = (1 639 ± 3) MPa
k_B = (1,391 ·10^–23 ± 7 ·10^–26) J/K	různé řády	k_B = (1,391 ± 0,007) ·10^–23 J/K
d = 35 ± 6 m	chybí závorka	d = (35 ± 6) m
a = 4,038 cm ± 0,02 mm	různé jednotky	a = (40,38 ± 0,02) mm
F = 235 ± 3 % N	za ± se uvádí absolutní chyba	F = (235 ± 7) N

Příklady pro domácí přípravu:

Příklad 1:: Při měření doby kmitu kyvadla byla získána následující data. Zpracujte tyto data měření a určete průměrnou dobu kmitu včetně odchylky.

č. m.	T / s
1	1,82
2	1,92
3	1,86
4	1,87
5	1,86
6	1,84
7	1,88
8	1,86
9	1,88
10	1,88
11	1,86
12	1,87
13	1,84
14	1,74
15	1,87
16	1,86
17	1,86
18	1,87
19	1,86
20	1,86

Tabulka experimentálních hodnot příkladu 1
lze stáhnout jako CSV soubor (textový soubor oddělený středníky)

Výsledek: T = (1,864 ± 0,009) s

Příklad 2:: Za stejných podmínek byl opakovaně měřen průměr kovové trubky. Zpracujte tyto data měření a určete průměr dané trubky včetně odchylky.

č. m.	d / cm
1	2,52
2	2,51
3	2,52
4	2,50
5	2,51
6	2,53
7	2,47
8	2,49
9	2,51
10	2,50
11	2,51
12	2,49
13	2,52
14	2,52
15	2,51

Tabulka experimentálních hodnot příkladu 2
lze stáhnout jako CSV soubor (textový soubor oddělený středníky)

Výsledek: d = (2,501 ± 0,009) cm

Chcete více potrénovat zpracování experimentálních dat přímého měření?

Vyzkoušejte procvičovací trenažér pro Nácvik zpracování exp. dat PŘÍMÉHO MĚŘENÍ