Druhy chyb a jejich vyjadřování

Základní pojmy

Naměřená hodnota

údaj odečtený na přístroji; je uváděn jako číselná hodnota a jednotka měřené veličiny.

Chyba (též „odchylka“, či „nejistota“)

číselně vyjádřený rozdíl mezi údajem přístroje a skutečnou hodnotou měřené veličiny.

Absolutní chyba

chyba vyjádřená číselně v jednotkách měřené nebo vytvářené veličiny. Označujeme ji symbolem Δ před danou veličinou – např. Δm, Δℓ apod.

Poměrná chyba (relativní)

poměr absolutní chyby ke skutečné hodnotě měřené veličiny. Pro označení používáme symbol δ s indexem dané veličiny – např. δ_m, δ_ℓ

Procentuální chyba (chyba vyjádřená v procentech)

poměr absolutní chyby ke skutečné hodnotě (tedy poměrná chyba) vyjádřený v procentech. Pro označení používáme symbol δ před danou veličinou – např. δm, δℓ

Druhy (typy) chyb

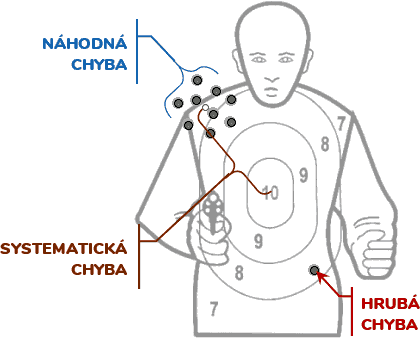
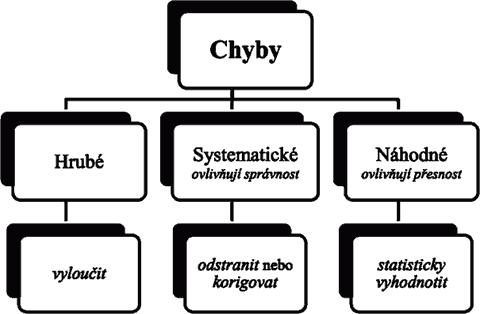
Systematické chyby (též Soustavné chyby)

ovlivňují výsledek měření zcela určitým způsobem, s jistou pravidelností. Systematičnost této chyby se projevuje tím, že měřené hodnoty veličiny jsou buď trvale větší, nebo menší, než je hodnota skutečná. Tyto odchylky lze přitom určit (odhadnout) a tak vliv soustavných chyb v podstatě vyloučit. Soustavné chyby mohou mít původ v použité metodě, v přístrojích anebo i v pozorovateli.

Náhodné chyby

se vyznačují tím, že působením velmi rozmanitých přesně nedefinovatelných vlivů se hodnoty určité veličiny, naměřené přibližně za stejných podmínek měření, poněkud liší. Může tu působit např. náhodná změna polohy oka, určitá malá změna teploty, tlaku. Nedodržení určitého tlaku měřicího šroubu u mikrometru (tento vliv se omezuje montáží kluzné spojky s „řehtačkou“, která zabezpečí přibližně stejný tlak). Také zde může působit nedokonalost předpokládaných tvarů při výrobě (např. průměr drátu musíme měřit v různých místech).

Hrubé chyby

vznikají nepozorností nebo přehlédnutím či poruchou měřicího přístroje, nevhodnou metodou měření, apod. Hrubé chyby se budeme snažit ze  souboru experimentálních dat vyloučit (např. opakovaným měření a následným vyloučením výrazně se odchylujících hodnot)

Měření fyzikálních veličin představuje v důsledku působení náhodných chyb statistický proces s náhodnou proměnnou. Pravděpodobnou hodnotu měřené fyzikální veličiny a její chyby tak lze určit statistickými metodami. Vliv náhodných chyb na výsledek měření klesá s počtem opakovaných měření.

Metody měření

Přímá metoda měření

Při použití přímé metody měření je výstupem přímo údaj hodnoty měřené veličiny v příslušných jednotkách. Je to tedy taková metoda měření, kdy je hodnota měřené veličiny získávána přímo, aniž je zapotřebí dodatečně provádět výpočty spočívající na závislosti měřené veličiny na veličinách jiného druhu. Příkladem může být měření rozměru posuvným měřidlem.

Nepřímá metoda měření

Při nepřímé metodě měření je hodnota některé veličiny určována na základě výsledků přímých měření veličin jiných druhů. Tyto veličiny jsou s vlastní měřenou veličinou vázány známými závislostmi. Mezi nepřímé metody se počítá také takové metody, kterými se přímo měří veličina jiného druhu než ta, kterou chceme určit, ale ke konečnému vyhodnocení nestačí převodní tabulky nebo grafy, ale musíme použít výpočet.