Měření na digitálním přístroji
Obecně převládá názor, že měření na digitálním přístroji je přece super přesné a že jej tedy zvládne i cvičená opička. Nechci zde znevažovat um a dovednosti některých primátů, ale letitý výzkum s jedinci živočišného druhu Homo sapiens sapiens ukazuje, že některé věci jsou trochu jinak, než si myslíme…

Je nezpochybnitelné, že práce s digitálními přístroji je do jisté míry snazší a pohodlnější než měření na přístrojích analogových. Je pravda, že se nemusíme trápit s přepočítáváním dílků stupnice a hodnotu na displeji snad správně přečte téměř každý. Na druhou stranu je třeba si připomenout, že měření na digitálním přístroji se v principu řídí stejnými fyzikálními pravidly, jako na přístroji analogovém. Tedy každý přístroj má určitou přesnost danou svou konstrukcí a technickým provedením, a také každý přístroj má své zobrazovací limity. Takže kupříkladu nevhodně zvolený měřicí rozsah může negativně ovlivnit přesnost měření, ať již měříme na displeji, nebo třeba „na tom s tou rafičkou“.
Dalo by se asi diskutovat o tom, zda někdy není dokonce lepší měřit na přístroji ručkovém, protože vidíme postupný nárůst výchylky, než jen civět na nic neříkající a stále poskakující čísla na displeji, ale to teď není účelem tohoto textu. Pojďme se podívat, jak správně měřit „na tom displeji“.
Jak bylo již řečeno, každý přístroj (i digitální) má určité měřicí limity a to co do rozsahu, tak především do přesnosti měření. U ručkových přístrojů tuto přesnost stanovuje tvz. třída přesnosti, u přístroje digitálního je tato přesnost zpravidla udána tabulkou v návodu nebo datovém listu. Takovým základním rozdílem je, že zatímco třída přesnosti se vztahuje k celkovému rozsahu ručkového přístroje, u přístrojů digitálních se zpravidla odchylka určuje z právě zobrazené (aktuálně čtené) hodnoty.
Ukážeme si to na následujícím přístroji. Na obrázku č. 1 vidíme digitální multimetr, který na displeji zobrazuje hodnotu 65,2. Občas se můžeme setkat i s případem, že poslední zobrazená číslice (zde ta 2 za desetinnou čárkou) různě rychle přeblikává na hodnoty jiné např. 65,3 nebo 65,1. To je takové to každému učiteli známé: „panečeli, co tam jako máme napsat, když vono to furt skáče…“
Takže, jak tedy měříme?

Obr. 1 – měření na digitálním přístroji
- Podíváme se na zvolenou měřenou veličinu a zvolený rozsah. Zde na obrázku 1 vidíme, že otočný přepínač multimetru je natočen do polohy stejnosměrného proudu a to konkrétně na rozsah 200 mA.
- Odečteme hodnotu z displeje. Nyní tedy již víme, že jsme naměřili stejnosměrný elektrický proud o velikosti 65,2 mA.
- Zkontrolujeme, zda máme nastavený vhodný rozsah. Nastavení rozsahu ovlivňuje nejen přesnost měření, ale i možnosti zobrazení. Možnosti displeje jsou omezené – zde maximálně 4 číslice. Na rozsahu 200 mA je asi tedy maximální zobrazitelná hodnota 200,0 (popř. 199,9). To odpovídá zobrazení na jedno desetinné místo. Pokud bychom dokázali zvolit rozsah do 100 mA, je jasné, že by maximální zobrazená hodnota na čtyřech místech displeje byla 99,99 (pokud je první segment displeje plnohodnotný). To je přesnost na dvě desetinná místa, takže by to bylo lepší.
Zde je však nižší rozsah pouze 20 mA, což je pro hodnotu 65,2 mA nepoužitelné, takže zůstaneme na zvoleném rozsahu. - Určíme přesnost (odchylku) změřené hodnoty. V návodu nebo datovém listu měřicího přístroje je třeba vyhledat kapitolu „Specifikace“ (nebo podobné), kde bychom měli najít potřebné informace. Mohou vypadat například následovně:
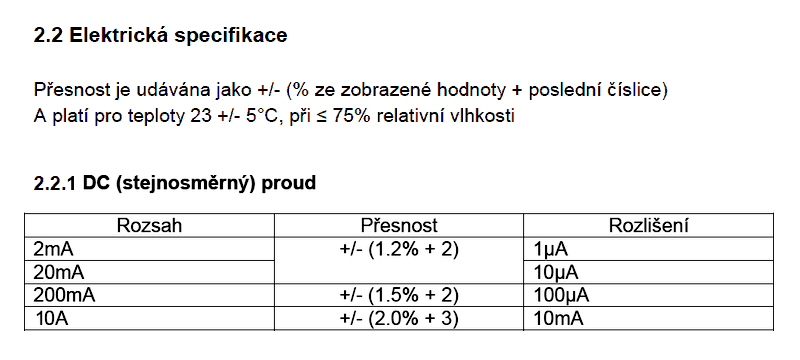
Jak vidíme z ukázky tohoto pro nás důležitého dokumentu, je přesnost digitálního přístroje nejen určena hodnotou procentuální odchylky z naměřené hodnoty, ale i určitým „paušálem“ v podobě neurčitosti na poslední číslici. Neurčitost poslední číslice je právě to pověstné: „…vono to furt skáče!“ Chyba zobrazení posledního místa vyplývá z rozlišovací schopnosti digitálního převodníku použitého v měřicím přístroji.
V našem případě (viz výše na obr. 2) je na stejnosměrném proudovém rozsahu 200 mA celková absolutní chyba měření dána procentuální chybou měření δI a chybou digitalizace ΔDIGI:
| Relativní chyba: | δI = 0,015 | (procentuální chyba δI = 1,5 %) | |
|---|---|---|---|
| Abs. chyba (plynoucí z δI): | ΔVI = 0,978 mA | (= δI · I = 0,015·65,2) | |
| Chyba digitalizace: | ΔDIGI = 0,2 mA | (+2 „skoky“ na poslední číslici při rozlišení 0,1 mA) |
|
|
Celková abs. chyba: ΔI |
= ΔVI + ΔDIGI =
|
- Získaný výsledek správně zaokrouhlíme. Pokud budeme s výsledkem dále pracovat, například využívat pro výpočet odporu, zaokrouhlíme absolutní chybu na dvě platné číslice. Výsledek by tedy bylo možné prezentovat v podobě:
I = (65,2 ± 1,2) mA
Pokud bychom naměřenou hodnotu proudu prezentovali jako celkový konečný výsledem, musíme hodnotu zaokrouhlit na stejný řád jako je první platná číslice absolutní odchylky, tedy:
I = (65 ± 1) mA
Podíváme-li se na právě získaný výsledek, asi musíme uznat, že to s tou přesností použitého digitálního přístroje nebude zas tak velký šlágr, jak jsme si mysleli při pohledu na svítící čísla na displeji.
Příklad pro domácí přípravu:

Obr. 3 – příklad pro domácí přípravu
Na obrázku číslo 3 je zobrazen multimetr, na kterém je právě měřena elektrická veličina.
V návodu měřicího přístroje je mimo jiného i následující tabulka:
| Rozsah | Přesnost | Rozlišení |
|---|---|---|
| 200 mV | ±(0,5 % + 2) | 0,1 mV |
| 2 V | 1 mV | |
| 20 V | 10 mV |
- Je měřeno na stejnosměrném nebo střídavém rozsahu?
- Určete, jaká veličina je právě měřena.
- Určete absolutní chybu měřené hodnoty.
- Uveďte výslednou hodnotu a zaokrouhlete ji jako hlavní výsledek.
- Výsledky:
- stejnosměrné napětí; U = 8,82 V; ΔU = 0,0641 V; U = (8,82 ± 0,06) V
